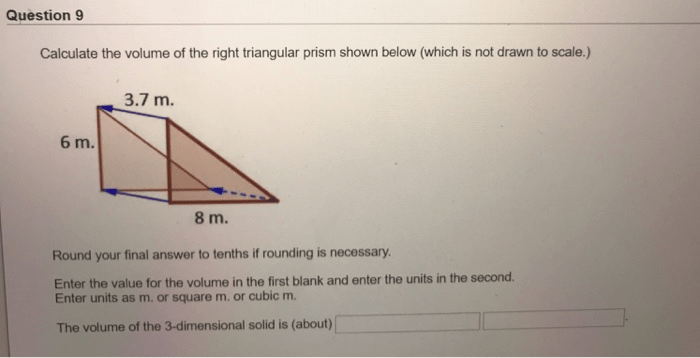
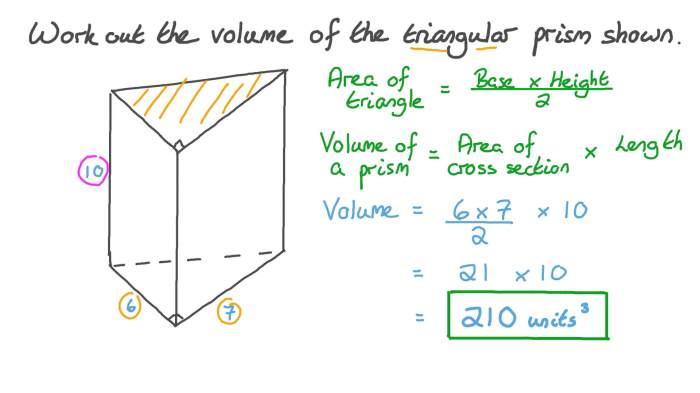
What is the volume of the triangular prism shown below – In this comprehensive guide, we delve into the fascinating realm of triangular prisms, unraveling the formula for calculating their volume and exploring the intricate relationship between their dimensions and shapes. Join us on this journey as we illuminate the practical applications of triangular prisms in diverse fields, unraveling the significance of their volume in real-world problem-solving.
Volume of a Triangular Prism
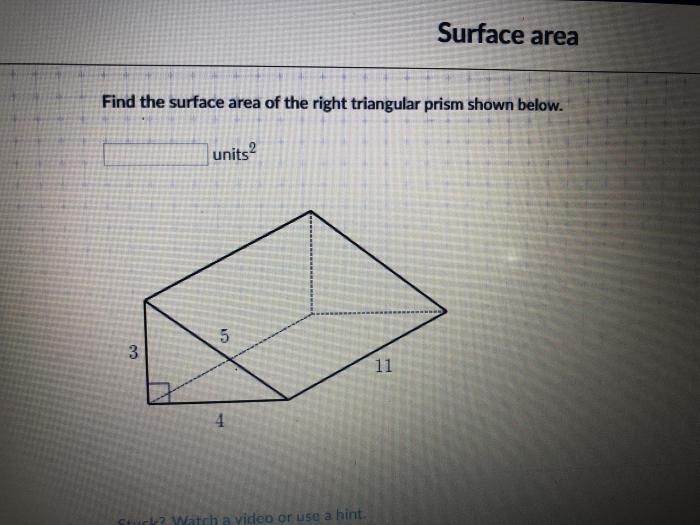
The volume of a triangular prism is calculated using the formula:
V = (1/2)
- B
- h
where:
- V is the volume of the prism in cubic units
- B is the area of the base of the prism in square units
- h is the height of the prism in linear units
For example, if a triangular prism has a base area of 10 square units and a height of 5 linear units, its volume would be:
V = (1/2)
- 10
- 5 = 25 cubic units
Dimensions of a Triangular Prism
The key dimensions of a triangular prism are:
- Length: The length of the base of the prism
- Width: The width of the base of the prism
- Height: The distance from the base of the prism to the opposite vertex
These dimensions are used to calculate the area of the base and the volume of the prism.
Shape of the Base
The base of a triangular prism can have different shapes, such as:
- Equilateral triangle
- Isosceles triangle
- Scalene triangle
The shape of the base affects the area of the base and, consequently, the volume of the prism.
Applications of Triangular Prisms
Triangular prisms have practical applications in various fields, including:
- Architecture: Triangular prisms are used in the design of roofs, bridges, and other structures.
- Engineering: Triangular prisms are used in the construction of bridges, towers, and other structures.
- Design: Triangular prisms are used in the design of furniture, toys, and other objects.
The volume of a triangular prism is an important factor in these applications, as it determines the amount of material needed and the structural integrity of the object.
Related Concepts, What is the volume of the triangular prism shown below
The volume of a triangular prism can be compared to the volume of other geometric shapes, such as:
- Cube: A cube is a three-dimensional shape with six square faces. The volume of a cube is calculated using the formula V = a³, where a is the length of one side of the cube.
- Cylinder: A cylinder is a three-dimensional shape with two circular faces and a curved surface. The volume of a cylinder is calculated using the formula V = πr²h, where r is the radius of the circular faces and h is the height of the cylinder.
The surface area of a triangular prism is the total area of all of its surfaces. The surface area of a triangular prism is calculated using the formula:
SA = B + 2(1/2)
- b
- h
where:
- SA is the surface area of the prism in square units
- B is the area of the base of the prism in square units
- b is the length of the base of the prism in linear units
- h is the height of the prism in linear units
The volume of a triangular prism can be used to solve real-world problems, such as:
- Calculating the amount of material needed to build a structure
- Determining the structural integrity of a bridge or other structure
- Designing objects that have a specific volume
Questions and Answers: What Is The Volume Of The Triangular Prism Shown Below
What is the formula for calculating the volume of a triangular prism?
Volume = (1/2) x base area x height
How does the shape of the base affect the volume of a triangular prism?
The area of the base determines the volume; different base shapes (e.g., equilateral, isosceles) result in varying base areas, thus influencing the prism’s volume.